Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography.
A "modular exponentiation" calculates the remainder when a positive integer b (the base) raised to the e-th power (the exponent), and the total quantity is divided by a positive integer m, called the modulus. In symbols, this is, given base b, exponent e, and modulus m, the modular exponentiation cis:
For example, given b = 5, e = 3, and m = 13, the solution c is the remainder of dividing by 13, which is the remainder of 125 / 13, or 8.
by 13, which is the remainder of 125 / 13, or 8.
If b, e, and m are non-negative, and b < m, then a unique solution c exists with the property 0 ≤ c < m.
Modular exponentiation can be performed with a negative exponent e by finding the modular multiplicative inverse d of b modulo m using the extended Euclidean algorithm. That is:
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography.
A "modular exponentiation" calculates the remainder when a positive integer b (the base) raised to the e-th power (the exponent), and the total quantity is divided by a positive integer m, called the modulus. In symbols, this is, given base b, exponent e, and modulus m, the modular exponentiation cis:

For example, given b = 5, e = 3, and m = 13, the solution c is the remainder of dividing
 by 13, which is the remainder of 125 / 13, or 8.
by 13, which is the remainder of 125 / 13, or 8.If b, e, and m are non-negative, and b < m, then a unique solution c exists with the property 0 ≤ c < m.
Modular exponentiation can be performed with a negative exponent e by finding the modular multiplicative inverse d of b modulo m using the extended Euclidean algorithm. That is:
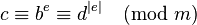 where e < 0 and
where e < 0 and 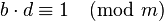
No comments:
Post a Comment