ME LECTURE NOTES-- Queueing analysis
In queueing
theory, a queueing model is used to approximate a real queueing
situation or system, so the queueing behaviour can be analysed mathematically.
Queueing models allow a number of useful steady
state performance measures to be determined,
including:
- the average number in the queue, or the system,
- the average time spent in the queue, or the system,
- the statistical distribution of those numbers or
times,
- the probability the queue is full, or empty, and
- the probability of finding the system in a particular
state.
These performance measures are important as issues or
problems caused by queueing situations are often related to customer
dissatisfaction with service or may be the root cause of economic losses in a
business. Analysis of the relevant queueing models allows the cause of queueing
issues to be identified and the impact of any changes that might be wanted to
be assessed.
Notation
Queueing models can be represented using Kendall's
notation:
A/B/S/K/N/Disc
where:
- A is the interarrival time distribution
- B is the service time distribution
- S is the number of servers
- K is the system capacity
- N is the calling population
- Disc is the service discipline assumed
Some standard notation for distributions (A or B) are:
- M for a Markovian
(exponential) distribution
- Eκ for an Erlang
distribution with κ phases
- D for Deterministic (constant)
- G for General distribution
- PH for a Phase-type
distribution
Models
Construction and analysis
Queueing models are generally constructed to represent
the steady state of a queueing system, that is, the typical, long
run or average state of the system. As a consequence, these are stochastic
models that represent the probability that a queueing system will be found in a
particular configuration or state.
A general procedure for constructing and analysing
such queueing models is:
- Identify the parameters of the system, such as the
arrival rate, service time, Queue capacity, and perhaps draw a diagram of
the system.
- Identify the system states. (A state will generally
represent the integer number of customers, people, jobs, calls, messages,
etc. in the system and may or may not be limited.)
- Draw a state transition diagram that represents the
possible system states and identify the rates to enter and leave each
state. This diagram is a representation of a Markov
chain.
- Because the state transition diagram represents the
steady state situation between state there is a balanced flow between
states so the probabilities of being in adjacent states can be related
mathematically in terms of the arrival and service rates and state
probabilities.
- Express all the state probabilities in terms of the
empty state probability, using the inter-state transition relationships.
- Determine the empty state probability by using the
fact that all state probabilities always sum to 1.
Whereas specific problems that have small finite state
models are often able to be analysed numerically, analysis of more general
models, using calculus,
yields useful formulae that can be applied to whole classes of problems.
Single-server queue
Single-server queues are, perhaps, the most commonly
encountered queueing situation in real life. One encounters a queue with a
single server in many situations, including business (e.g. sales clerk),
industry (e.g. a production line), transport (e.g. a bus, a taxi rank, an
intersection), telecommunications (e.g. Telephone line), computing (e.g. processor
sharing). Even where there are multiple servers handling the situation it is
possible to consider each server individually as part of the larger system, in
many cases. (e.g A supermarket checkout has several single server queues that
the customer can select from.) Consequently, being able to model and analyse a
single server queue's behaviour is a particularly useful thing to do.
Poisson
arrivals and service
M/M/1/∞/∞ represents a single server that has unlimited queue
capacity and infinite calling population, both arrivals and service are Poisson
(or random) processes, meaning the statistical distribution of both the
inter-arrival times and the service times follow the exponential distribution.
Because of the mathematical nature of the exponential distribution, a number of
quite simple relationships are able to be derived for several performance
measures based on knowing the arrival rate and service rate.
This is fortunate because, an M/M/1 queuing model can
be used to approximate many queuing situations.
Poisson
arrivals and general service
M/G/1/∞/∞ represents a single server that has unlimited queue
capacity and infinite calling population, while the arrival is still Poisson
process, meaning the statistical distribution of the inter-arrival times still
follow the exponential distribution, the distribution of the service time does
not. The distribution of the service time may follow any general statistical
distribution, not just exponential. Relationships are still able to be derived
for a (limited) number of performance measures if one knows the arrival rate
and the mean and variance of the service rate. However the derivations a
generally more complex.
A number of special cases of M/G/1 provide specific
solutions that give broad insights into the best model to choose for specific
queueing situations because they permit the comparison of those solutions to
the performance of an M/M/1 model.
Multiple-servers
queue
Multiple (identical)-servers queue situations are
frequently encountered in telecommunications or a customer service environment.
When modelling these situations care is needed to ensure that it is a multiple
servers queue, not a network of single server queues, because results may
differ depending on how the queuing model behaves.
One observational insight provided by comparing
queuing models is that a single queue with multiple servers performs better
than each server having their own queue and that a single large pool of servers
performs better than two or more smaller pools, even though there are the same
total number of servers in the system.
One simple example to prove the above fact is as
follows: Consider a system having 8 input lines, single queue and 8 servers.The
output line has a capacity of 64 kbit/s. Considering the arrival rate at each
input as 2 packets/s. So, the total arrival rate is 16 packets/s. With an
average of 2000 bits per packet, the service rate is 64 kbit/s/2000b = 32
packets/s. Hence, the average response time of the system is 1/(μ-λ) =
1/(32-16) = 0.0667 sec. Now, consider a second system with 8 queues, one for
each server. Each of the 8 output lines has a capacity of 8 kbit/s. The
calculation yields the response time as 1/(μ-λ) = 1/(4-2) = 0.5 sec. And the
average waiting time in the queue in the first case is ρ/(1-ρ)μ = 0.25, while
in the second case is 0.03125.
Infinitely many
servers
While never exactly encountered in reality, an infinite-servers
(e.g. M/M/∞) model is a convenient
theoretical model for situations that involve storage or delay, such as parking
lots, warehouses and even atomic transitions. In these models there is no
queue, as such, instead each arriving customer receives service. When
viewed from the outside, the model appears to delay or store each customer
for some time.
Queueing System Classification
With Little's Theorem, we have developed some basic
understanding of a queueing system. To further our understanding we will have
to dig deeper into characteristics of a queueing system that impact its
performance. For example, queueing requirements of a restaurant will depend
upon factors like:
- How do customers arrive in the restaurant? Are
customer arrivals more during lunch and dinner time (a regular
restaurant)? Or is the customer traffic more uniformly distributed (a
cafe)?
- How much time do customers spend in the restaurant?
Do customers typically leave the restaurant in a fixed amount of time?
Does the customer service time vary with the type of customer?
- How many tables does the restaurant have for
servicing customers?
The above three points correspond to the most
important characteristics of a queueing system. They are explained below:
Arrival Process
|
|
Service Process
|
|
Number of Servers
|
|
Based on the above characteristics, queueing systems
can be classified by the following convention:
A/S/n
Where A is the arrival process, S is the service
process and n is the number of servers. A and S are can be any of the
following:
M (Markov)
|
Exponential probability density
|
D (Deterministic)
|
All customers have the same value
|
G (General)
|
Any arbitrary probability
distribution
|
Examples of queueing systems that can be defined with
this convention are:
- M/M/1: This is the simplest queueing system to
analyze. Here the arrival and service time are negative exponentially
distributed (poisson process). The system consists of only one server.
This queueing system can be applied to a wide variety of problems as any system
with a very large number of independent customers can be approximated as a
Poisson process. Using a Poisson process for service time however is not
applicable in many applications and is only a crude approximation. Refer
to M/M/1
Queueing System for details.
- M/D/n: Here the arrival process is poisson and
the service time distribution is deterministic. The system has n servers.
(e.g. a ticket booking counter with n cashiers.) Here the service time can
be assumed to be same for all customers)
- G/G/n: This is the most general queueing
system where the arrival and service time processes are both arbitrary.
The system has n servers. No analytical solution is known for this queueing
system.
Markovian arrival processes
In queuing
theory, Markovian arrival processes are used to model the arrival
customers to queue.
Some of the most common include the Poisson process,
Markovian arrival process and the batch Markovian arrival process.
Markovian arrival processes has
two processes. A continuous-time
Markov process j(t), a Markov
process which is generated by a generator or rate matrix, Q. The other process is a counting process N(t),
which has state space
 is the set of all
natural
numbers). N(t) increases every
time there is a transition in j(t)
which marked.
is the set of all
natural
numbers). N(t) increases every
time there is a transition in j(t)
which marked.
Poisson process
The Poisson
arrival process or Poisson
process counts the number of arrivals, each of which has a exponentially
distributed time between arrival. In the most general case this can be
represented by the rate matrix,
Markov arrival process
The Markov arrival process (MAP) is a
generalisation of the Poisson process by having non-exponential
distribution sojourn
between arrivals. The homogeneous case has rate matrix,
Little's law
In queueing
theory, Little's result, theorem, lemma, or law
says:
The average number of customers in a stable system
(over some time interval), N, is equal to their average arrival rate, λ,
multiplied by their average time in the system, T, or:
It is also a comparatively recent result - it was
first proved by John
Little, an Institute
Professor and the Chair of Management Science at the MIT
Sloan School of Management, in 1961.
Handily his result applies to any system, and
particularly, it applies to systems within systems. So in a bank, the queue
might be one subsystem, and each of the tellers another subsystem, and Little's
result could be applied to each one, as well as the whole thing. The only
requirement is that the system is stable -- it can't be in some transition state
such as just starting up or just shutting down.
Mathematical formalization of Little's theorem
Let α(t) be to some system in the interval
[0, t]. Let β(t) be the number of departures from the same
system in the interval [0, t]. Both α(t) and β(t) are
integer valued increasing functions by their definition. Let Tt
be the mean time spent in the system (during the interval [0, t])
for all the customers who were in the system during the interval [0, t].
Let Nt be the mean number of customers in the system over the
duration of the interval [0, t].
If the following limits exist,
and, further, if λ = δ then Little's theorem holds, the limit
exists and is given by Little's theorem,
Ideal Performance






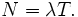

No comments:
Post a Comment